【单元教学】高中数学人教A版必修第二册7.1 复数的概念
时间:2023-04-03 作者: 阅读:
一、内容解析
(说明:通过内容解析确定单元教学重点)
内容的本质:通过解方程引入了复数,研究了复数的表示与运算,几何意义,将实数系扩充成复数系。复数的本质是由实数(已有知识)构成的有序实数对,因此复数与复平面内的点是一一对应的,与复平面内以原点为起点的向量也是一一对应的,由复数的向量表示可以进一步得到复数的三角形式。
因此,确定本单元课的教学重点:
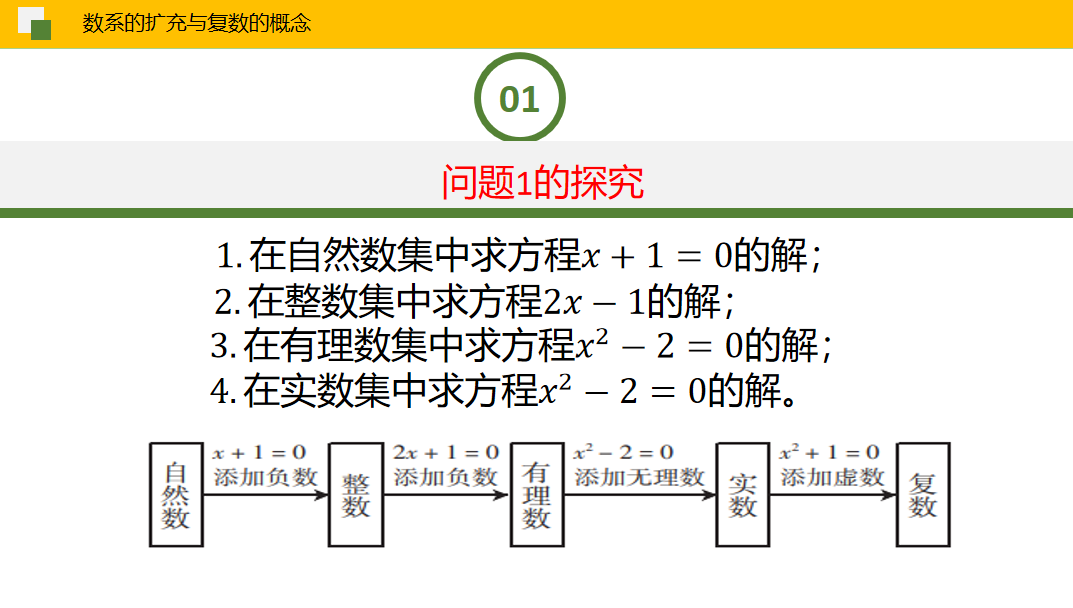
(1)梳理数系扩充的过程与“规则”,类比自然数集到实数集的扩充,引入复数。
(2)理解复数的概念与几何意义,复数的四则运算。
二、目标解析
(说明:通过目标解析明确达成单元目标的标志)
达成上述目标的标志是:
(1)能够通过方程的解,感受引入复数的必要性,学生能说明虚数ⅰ的由来、复数代数形式、复数分类,会用Venn图表示复数集、实数集、虚数集、纯虚数集之间的关系;能利用复数概念和复数相等的含义解决相关的简单问题。
(2)能从复平面的有序实数对去理解复数的几何意义。从几何意义理解共轭复数,复数的模等概念。理解复数的模的几何意义,实质转化为两实数对之间的距离问题。
(3)能准确计算复数的加减乘除运算,灵活运用复数的运算律;理解复数的加减运算的实质是向量的坐标运算;了解复数的乘除运算就是平面向量的旋转、伸缩。
(4)通过有序实数对角度,引入角,从解三角形方向推出复数的三角形式,明白辐角意义。复数的乘除运算的三角表示,实质是向量的旋转问题,通过数形结合,能够说清楚乘除后的复数的模与辐角的变化规律。
三、教学问题诊断分析
(说明:通过问题诊断确定本单元难点)
学生已经学会在实数范围内求解一元二次方程,高中阶段已经学习了数集之间的包含关系、向量、三角函数等内容,但知识是零碎、分散的,对数的发展的历史和规律缺乏整体认识与理性思考,学生不太了解数系扩充的“规则”,也不适应复数的代数形式是两项之和。对于复数乘除的几何意义,复数乘除运算的三角形式的几何意义,实质是旋转与伸缩,学生对此会感觉到抽象。
因此本单元的教学难点为:复数的引入,复数的代数形式是两项之和形式。复数乘除运算的三角表示及其几何意义。
四、课时教学设计
(本单元共安排6课时。)
第1课时 数系的扩充与复数的概念
教学过程设计
问题1